단일층 신경망(single layer neural network) 구현하기

오늘은 정말 간단한 딥러닝 기법인 '단일층 신경망'에 대해 공부해봅시다!

수치를 예측하는 regression 문제와 범주를 예측하는 binary 문제 두가지를 다뤄볼 것 입니다.

엄청나게 간단합..니...다.. ㅋ

1. 선형 회귀(linear regression)

선형회귀는 어떤 값을 예측하는 문제를 다룹니다.

선형 회귀를 위한 뉴런을 만들기 위해서 경사 하강법 알고리즘을 파이썬으로 짜볼 것 입니다.

원리는 간단합니다.

1. 그냥 저희가 구해야하는 변수인 w와 b를 아무런 수로 넣고

2. loss가 최대한 작아지도록 w와 b값을 수정합니다.

3. 이걸 epochs 만큼 반복합니다. ( epochs는 지정할 수 있습니다.)

 

여기서 알아두어야 할 것은 정방향 계산과 역방향 계산 두가지가 존재한다는 점 입니다.

정방향 계산은 y를 예측하기 위한 식이고, 역방향 계산은 w와 b값을 조정하기 위한 식입니다.

그림으로 도식화 하면 다음과 같습니다.

업데이트식은 loss function을 미분하면 됩니다. (업데이트식 도출은 to be continue...)

 

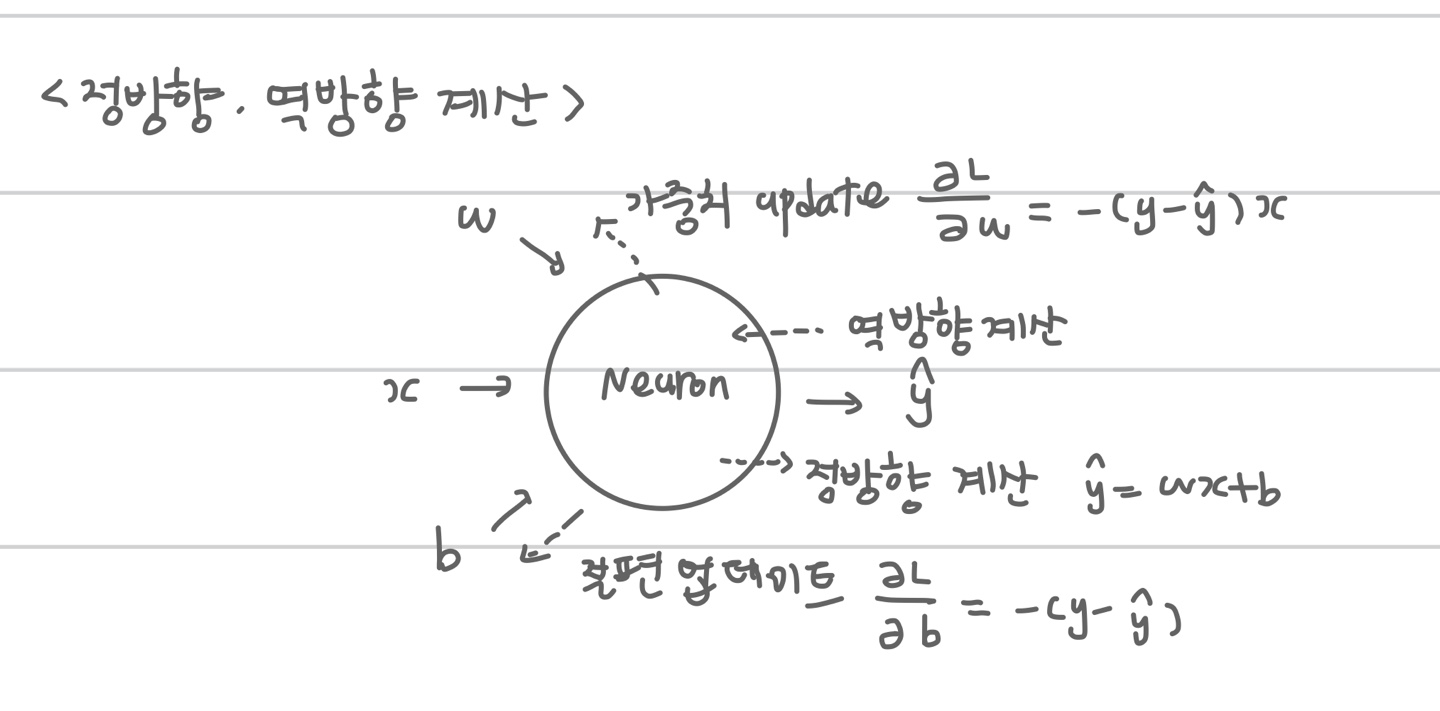
신경망으로 나타낸 선형회귀는 입력층과 출력층만 존재합니다. (단일층 신경망)

더 복잡하게 들어가면 이제 은닉층이 추가되는 것입니다. (다층 신경망)

다층 신경망을 다룬 글도 나중에 적어보겠습니다. (again to be continue...)

경사 하강법 알고리즘을 파이썬 클래스로 만들면 다음과 같습니다.

이름은 Neuron이라고 지어줬습니다.

class Neuron:
    def __init__(self):
        self.w = 1.0
        self.b = 1.0

    # 정방향 계산
    def forpass(self,x):
        y_hat = x*self.w + self.b
        return y_hat

    # 역방향 계산
    def backprop(self,x,err):
        w_grad = x*err
        b_grad = 1*err
        return w_grad, b_grad

    def fit(self, x, y, epochs=100):
        for i in range(epochs):
            for x_i, y_i in zip(x,y):
                y_hat = self.forpass(x_i)
                err = -(y_i - y_hat)
                w_grad, b_grad = self.backprop(x_i,err)
                self.w -= w_grad
                self.b -= b_grad

입력하는 x값과 y값을 지정해준 후 실행을 시키면 됩니다.

neuron = Neuron()
neuron.fit(x,y)

물론 데이터를 train과 test로 나눠주는 것은 꼭 필요합니다.

이 코드에는 test로 성능을 평가하는 함수는 포함되어 있지 않습니다.

 

 

 

 

2. 이진분류(binary classification)

이진분류는 데이터를 True나 False로 구분하는 문제를 말합니다.

이진분류의 퍼셉트론 구조를 살펴보면 이전의 회귀 구조에서 무언가 추가된 것을 볼 수 있습니다.

로지스틱 회귀

바로 계단함수(step function)이 추가가 된 것인데요. ( 그림에선 임계함수라고 표현되어 있습니다.)

계단함수는 샘플을 이진분류하기 위해 필요한 함수입니다.

 

로지스틱 회귀는 선형함수를 통과해 활성화함수를 거친 후 임계함수로 예측합니다.

활성화함수는 비선형 함수를 사용해 선형함수를 변형시켜줍니다.

여기선 활성화함수로 시그모이드 함수를 사용했습니다.

 

여기서도 업데이트 식을 위해 미분을 해주면 되는데, 함수를 3가지 거치다 보니 추론이 살짝 복잡합니다.

하지만 결과적으로 업데이트 식은 아까의 회귀식과 비슷합니다.

 

로지스틱 회귀를 python class로 구현해보았습니다.

class LogisticNeuron:
    def __init__(self):
        self.w = None
        self.b = None

    def forpass(self, x):
        z = np.sum(x*self.w)+self.b
        return z

    def backprop(self, x, err):
        w_grad = x*err
        b_grad = 1*err
        return w_grad, b_grad

    def activation(self,z):
        a = 1/(1+np.exp(-z))
        return a

    def fit(self, x, y, epochs=100):
        self.w = np.ones(x.shape[1])
        self.b = 0
        for i in range(epochs):
            for x_i, y_i in zip(x,y):
                z=self.forpass(x_i)
                a=self.activation(z)
                err = -(y_i-a)
                w_grad, b_grad = self.backprop(x_i,err)
                self.w -= w_grad
                self.b -= b_grad

    def predict(self,x):
        z = [self.forpass(x_i) for x_i in x]
        a = self.activation(np.array(z))
        return a>0.5

predict 함수도 추가해서 성능평가도 가능하게 되었습니다.

neuron = LogisticNeuron()
neuron.fit(x_train, y_train)

np.mean(neuron.predict(x_test) == y_test)

 

 

 

이제까지 단일층 신경망이였습니다.

딥러닝의 아주 기초중에 기초를 정리해보았습니다.